Stateczność prętów i wyboczenie prętów – teoria, obliczenia, praktyka

Czy kiedykolwiek zastanawiałeś się ile kilogramów możesz położyć na pustej puszce po piwie, tak aby wytrzymała 🏋? Czy zastanawiałeś się, dlaczego przy pewnym obciążeniu puszki, gdy w nią pstrykniesz palcem nagle ulega zgnieceniu ? Jeśli tak to zastanawiałeś się nad pojęciami związanymi ze statecznością prętów i wyboczeniem prętów…

Jakie czynniki wpływają na stateczność pręta (a w zasadzie utratę stateczności prętów)? Jak liczy się wyboczenie prętów? Jak liczy się siłę krytyczną i naprężenia krytyczne? Zapraszam na dawkę wiedzy z mechaniki klasycznej ⚙

Co to jest stateczność pręta?

Zacznijmy najpierw od podstaw i wyjaśnijmy podstawowe pojęcie, czyli: „czym jest stateczność prętów?”

Stateczność prętów to pojęcie, o którym najczęściej mówi się w budownictwie i mechanice. Zjawisko to polega na tym, że pręty zachowują stałą równowagę w czasie ich obciążania. Innymi słowy pręty są stateczne, gdy pod wpływem obciążeń zachowują swój kształt lub po odjęciu tego obciążenia – wracają do poprzedniego kształtu = nic się z nimi nie dzieje, a tym samym nasza konstrukcja (budowla lub maszyna) nie ulega destrukcji.

Co to jest wyboczenie prętów

Pojęcie wyboczenia prętów jest bardzo ważnym zjawiskiem, na które należy zwrócić szczególną uwagę w czasie projektowania maszyn i budowli, w których występują wszelkiego rodzaju konstrukcje oparte na belkach, czy ramach.

W poprzednim akapicie dowiedziałeś się, co to jest stateczność prętów. Wyboczenie prętów zachodzi wtedy, gdy pręty tracą swoją stateczność na skutek zbyt dużego obciążenia. Mogą to być np. za duże obciążenia osiowe. Dochodzi wówczas do poprzecznego odkształcenia pręta (prostopadłego do osi wzdłużnej pręta) = pręty się tak jakby ‘wyginają’.

Czynniki wpływające na powstawanie zjawiska wyboczenia prętów

Zanim przejdziemy do matematycznych rozważań i analizy wyboczenia prętów, warto zastanowić się, co tak naprawdę wpływa na to, że pręty ulegają wyboczeniu i tracą swoją równowagę stateczną (mówi się, że przechodzą wtedy w stan ‘chwiejny’).

Pomijając właściwości fizyczno-chemiczne pręta, czynnikami wpływającymi na zjawisko wyboczenia prętów są szczególnie:

A. Siła krytyczna osiowa
B. Występowanie mimośrodu podczas ściskania
C.Występowanie dodatkowego obciążenia poprzecznego

Skutki wyboczenia prętów – teoria

Żeby dobrze zrozumieć zagrożenia jakie niesie ze sobą zjawisko wyboczenia prętów musimy wejść nieco w teorię 😱…

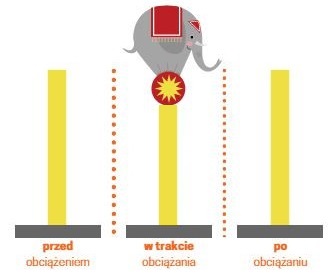
Wyobraźmy sobie stalowy pręt, który jest ściskany rosnącą siłą. Na początku pręt bardzo minimalnie skraca się sprężyście (tzn. że po ‘zabraniu’ tej siły wraca do poprzedniego kształtu). Do czasu…

W pewnym momencie siła przekracza tzw. wartość krytyczną (symbolizuje to pręt ze słonikiem i liściem) i pręt zaczyna się odkształcać poprzecznie. Na początku sprężyście (czyli może powrócić do poprzedniego kształtu = bezpiecznie), ale później dochodzi do stałego odkształcenia poprzecznego i pręt ulega wyboczeniu (czyli tak jakby zgina się w bok). Wówczas okazuje się, że siła potrzebna do dalszego zginania pręta maleje.

Dlaczego? Rozważmy rozkład sił w wybaczającym się pręcie:

Doszło do tego, że siła obciążająca nasz układ działa teraz z pewnym mimośrodem (kierunek działania siły nie leży idealnie w osi pręta – czynnik wpływający na stateczność pręta ‘B’). Powstało dodatkowe obciążenie pręta momentem zginającym, co z punktu widzenia wytrzymałości materiałów jest bardzo niekorzystne.

Skutki wyboczenia prętów – praktyka

Jak się możesz domyślić w praktyce skutki wyboczenia prętów są katastrofalne. Jeśli bowiem dojdzie do wyboczenia jednego pręta z całej konstrukcji, wówczas najczęściej niesie to za sobą gwałtowne zniszczenia całej maszyny lub danego podzespołu, na które działa dane obciążenie.

Poniżej możesz zobaczyć, jak NASA bada wyboczenie swoich rakiet, dzięki czemu zespół konstruktorów może zoptymalizować konstrukcję lub dobrać lepsze materiały:

Warto też wspomnieć o tym, że budownictwie wyboczenie pręta (a kolejno prętów) może mieć tragiczne skutki, szczególnie gdy mówimy o bardzo odpowiedzialnych konstrukcjach np. takich, jak mosty. Przed ‘odkryciem’ i rozpoczęciem badań tego zjawiska niszczenie się mostów było dość powszechnym zjawiskiem.

Czynniki wpływające na wyboczenie prętów

Mam nadzieję, że masz już w głowie przynajmniej poglądowo wyjaśnione czym jest wyboczenie prętów. Możemy zatem przejść do analizy wyboczenia prętów, dlatego rozpoczniemy od omówienia poszczególnych czynników wyboczenia prętów:

Siła krytyczna osiowa w wyboczeniu prętów

Pierwszym czynnikiem, od którego zaczniemy analizę wybroczeń prętów jest siła krytyczna 💪, która działa idealnie w osi pręta.  Siła krytyczna – określa wartość siły przy której dochodzi do wyboczenia prętów (pręty zaczynają się wyginać).

Obliczenia siły krytycznej i naprężeń krytycznych – wzór Eulera

W Internecie możesz znaleźć wiele opracowań, w których wyprowadzono poniższy wzór (tzw. wzór Eulera). Dzięki niemu możesz obliczyć siłę krytyczną dla danego pręta. Warto jednak zaznaczyć, że wzór ten stosuje się wyłącznie dla stanu sprężystego materiału tj. wtedy, gdy nie dochodzi jeszcze do groźnych stałych odkształceń po odjęciu obciążenia – pręt wraca wtedy do swojego pierwotnego kształtu.

Wzór Eulera ma następującą postać:

przy czym:

Pkr – siła krytyczna [N]

E – moduł Younga dla danego materiału [Pa]

J – moment bezwładności przekroju pręta [m^4]

Lw – długość wyboczeniowa pręta (uwaga: zależna od sposobu zamocowania) [m]

Aby otrzymać wzór na naprężenia krytyczne wystarczy, że siłę krytyczną podzielimy przez pole (przekrój poprzeczny) naszego pręta:

przy czym:

σkr – naprężenia krytyczne [Pa]

A – pole poprzecznego przekroju pręta [m^2]

Jak widzisz wzorek jest prosty i przyjemny, ale musisz zwrócić szczególną uwagę na parametr ’Lw’ czyli długość wyboczeniową…

Długość wyboczeniowa pręta

Zapamiętaj sobie, że długość wyboczeniowa pręta NIE JEST równa długości pręta! Wynika to z bardziej zaawansowanych zależności matematycznych, których tutaj nie przedstawiamy (nie będziemy komplikować i mieszać Ci w głowie), dlatego przejdziemy od razu do konkretów…

Wzór na długość wyboczeniową pręta jest następujący:

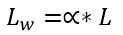
przy czym:

Lw- długość wyboczeniowa pręta [m]

α – współczynnik długości wyboczeniowej zależny od zamocowania pręta

L – długość pręta [m]

Współczynnik długości wyboczeniowej pręta ‘α’

Zatrzymajmy się teraz na współczynniku długości wyboczeniowej pręta. Współczynnik długości wyboczeniowej pręta określa się w zależności od tego, jak zamocowany jest nasz pręt (jakie stopnie swobody zostały mu odebrane).

Aby dobrać współczynnik długości wyboczeniowej pręta trzeba zatem skorzystać ze specjalnych, wykonanych przez matematyków tabel lub rysunków i dobrać dany przypadek do odpowiednika w tabeli lub na rysunku. Na poniższym rysunku przedstawiamy Ci wspomniane, różne konfiguracje mocowania pręta wraz z odpowiadającym jemu współczynnikiem wyboczeniowym α:

Utrata stateczności prętów i punkt bifurkacji

Warto wspomnieć o tym, że pręty zamieniają swoją równowagę ze stałej na tzw. chwiejną. Dzieje się tak ponieważ pręty nie są idealnie okrągłe i zawsze występuje mimośród dla siły ściskającej (czynnik B opisany wyżej).

Czasem jednak istnieją układy, w których dostarczana jest nawet niewielka ilość energii przez siłę poprzeczną (działającą na bok pręta). Przykładem takiej siły może być wiejący, boczny wiatr na daną konstrukcję. Siła taka sprawia, że ciało zamienia swój stan z równowagi stałej na chwiejną. Układy takie nazywa się układami o niedostatecznej stateczności.

Przyjrzyjmy się teraz temu ciekawemu wykresowi:

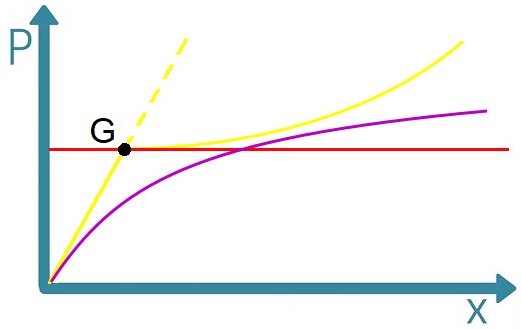
przy czym:

P – to siła przykładana do pręta,

x –  to przemieszczenie jednego, ruchomego końca pręta (punkt B zbliża się do punktu A)

Linia pozioma czerwona – odnosi się do wartości siły krytycznej po której przekroczeniu następuje ugięcie pręta (wyboczenie pręta).

Linia żółta – prezentuje zależność siły od ugięcia w przypadku idealnie centralnie przyłożonej siły, przy braku siły poprzecznej (teoretyczny przypadek)

Punkt G – miejsce przecięcia się linii poziomej czerwonej i linii żółtej, czyli punkt bifurkacji

Linia fioletowa – prawdziwy przypadek obciążania prętów i wyboczenia prętów

O co chodzi w tym wykresie? 🤔

Wykres przedstawia zależność między wartością siły ściskającej pręt, a przemieszczeniem jednego końca pręta do drugiego końca (punkt B zbliża się do punktu A).

Na początku ściskając pręt poruszamy się po linii grubej żółtej. Wraz ze wzrostem siły ściskającej P dochodzi do proporcjonalnego skracania się pręta. Gdy dochodzimy do siły krytycznej (punkt G – punkt bifurkacji = punkt rozdwojenia) w teorii mamy wtedy dwie opcje…

1. Albo nasz pręt dalej idealnie się kurczy (linia kreskowa cienka żółta)
2. Albo nasz pręt ulegnie wygięciu i dojdzie do jego wyboczenia (dalsza część linii żółtej grubej). Wówczas widać, że mały przyrost siły powoduje znaczny wzrost przemieszczenia punktu B – wynika to ze wyjaśnionych wcześniej obciążeń (wtedy gdy wspominałem o mimośrodzie i momencie zginającym).

Linia fioletowa przedstawia prawdziwy przypadek obciążania prętów siłami ściskającymi 👌 – gdy zakładamy mimośród, czyli przesunięcie przyłożenia siły w stosunku do osi pręta już na samym początku obciążania pręta.

W rzeczywistości tak właśnie zachowują się ściskane i wybaczające się pręty, gdyż spełnienie warunku centralnego przyłożenia jest niezwykle trudne. No dobra… niemożliwe.

Dodam tylko, że im większy jest mimośród tym linia fioletowa będzie zbliżać się do linii czerwonej (rośnie moment zginający). Im mniejszy mimośród to linia fioletowa będzie zbliżona do linii żółtej grubej.

Smukłość pręta i wyboczenie posprężyste

Jak wspomniałem wcześniej wzór Eulera stosujemy wyłącznie w zakresie sprężystym. Kiedy jednak przechodzimy do obliczeń w zakresie sprężysto-plastycznym (posprężystym) stosuje się nieco inne wzory (aproksymacje=przybliżenia) do wyznaczenia naprężeń krytycznych. O tym za chwilkę…

W akapicie poświęconym wzorowi Eulera dowiedzieliśmy się, że naprężenia krytyczne wyraża się zależnością:

Wzór ten można nieco uprościć stosując dwa współczynniki.

Jednym z nich jest promień bezwładności przekroju poprzecznego pręta ‘i’:

Drugim jest smukłość pręta ‘λ’. Smukłość pręta opisuje wzór:

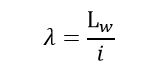
Dzięki tym dwóm zależnościom możemy dokonać prostego przekształcenia wzoru na naprężenia krytyczne dla wybaczanego pręta:

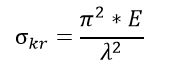
Popatrzmy na wykres przedstawiający zależność naprężeń krytycznych od smukłości pręta ulegającego wyboczeniu…

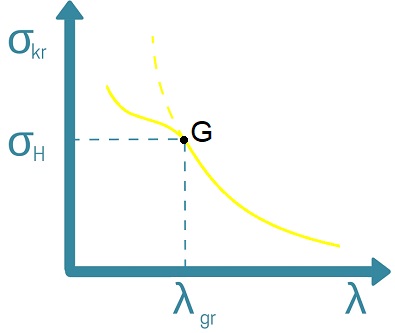
Linia żółta gruba – przedstawia krzywą doświadczalną przy wyginaniu pręta

Punkt G – stanowi granicę stanu sprężystego i sprężysto-plastycznego (posprężystego). Jest to miejsce, w którym dla smukłości granicznej λgr występują naprężenia σH określające granicę proporcjonalności (po przekroczeniu tego naprężenia odkształcenia nie są już proporcjonalne).

Linia żółta kreskowa, cienka przedstawia krzywą Eulera – hiperbola (postać wynika z w/w wzoru). Widać, że krzywa ta w praktyce pokrywa się z praktycznymi doświadczeniami wyłącznie w stanie sprężystym, tj. gdy λ > λgr

Co jeśli chcemy liczyć naprężenia w stanie posprężystym?

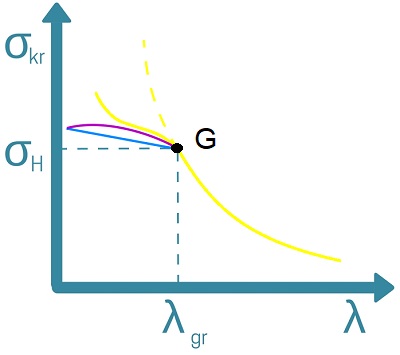
Wówczas stosujemy tzw. wzory empiryczne (wyznaczone na podstawie doświadczeń), czyli wzory które aproksymują (przybliżają) obliczenia do wyników rzeczywistych. Najczęściej korzysta się z dwóch wzorów:

Wzór Tetmajera – Jasińskiego (linia niebieska):

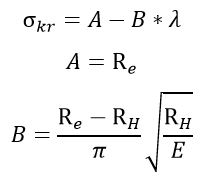
przy czym:

R_e – granica plastyczności

R_H  – granica proporcjonalności

E – moduł Younga

lub

wzór Johnsona-Ostenfolda (linia fioletowa):

Przykład obliczeń wyboczenia pręta

W tym prostym przykładzie wykonamy dla Ciebie przykładowe obliczenia dla zjawiska wyboczenia pręta o następujących wymiarach:

– średnica: 100 mm = 0,1 m (promień R = 0,05 m)

– długość: 2000 mm = 2 m

– materiał: stal (moduł Younga stali: E = 2,10 * 10^11 Pa)

– rodzaj utwierdzenia: pręt całkowicie utwierdzony w dolnej części

Zadanie polega na tym, aby obliczyć masę słonia, który spowoduje wyboczenie pręta (no dobra… na studiach będziesz raczej musiał obliczyć siłę krytyczną dla wybaczania opisanego wyżej pręta ‘P’ i na tym zakończymy)

Wróćmy się do wzoru na siłę krytyczną wyboczenia pręta:

Widać, że w zasadzie wszystkie dane mamy podane, jak na tacy, oprócz dwóch parametrów.

• α – współczynnik wyboczenia pręta
• J – moment bezwładności przekroju pręta

Zgodnie z powyższymi moimi ‘wypocinami’ i grafikami widać, że dla opisywanego pręta (utwierdzonego tylko na dole) współczynnik wyboczenia będzie równy 2 (α = 2).

Kolejno ze specjalnych tabel dobieramy moment bezwładności przekroju ‘J’ dla okrągłego pręta (wiemy, że jest okrągły, ponieważ w zadaniu mamy informację o jego średnicy). Moment bezwładności przekroju dla okrągłego pręta wraża się wzorem:

przy czym:

R – promień pręta [m]

Wróćmy teraz do wzoru na siłę krytyczną wyboczenia pręta i wstawiajmy po kolei:

Uff… teraz wstawiamy dane i jak to się mówi ‘jesteśmy w domu’:

_{Wyszło nam, że siła krytyczna dla takiego pręta wynosi 635 kN (kiloniutonów) / 0,635 MN (meganiutonów).}

Badania komputerowe wyboczenia pręta – analiza MES

Teraz zasymulujemy dla Ciebie co się dzieje z prętem, który poddamy wyboczeniu w… komputerze 💪. Przeprowadzimy symulację – analizę MES (metoda elementów skończonych). Symulacje takie najczęściej przeprowadza się dla bardziej zaawansowanych konstrukcji, ale fajnie można też na nich przedstawić różne zjawiska. Na przykład stateczność prętów i wyboczenie prętów.

Najpierw zamodelowaliśmy prosty pręt, zgodnie z opisem wyżej. Ustawiliśmy też dla niego odpowiedni materiał (stal) – zdjęcie po lewej. Następnie dokonaliśmy ustawień do symulacji. Między innymi: związaliśmy (unieruchomiliśmy komputerowo) pręt na dole, ustawiliśmy grawitację pionowo w dół, włączyliśmy też siłę ściskającą – zdjęcie po prawej.

Jesteśmy gotowi do przeprowadzenia komputerowej symulacji wyboczenia pręta….. Poniżej możesz zobaczyć, jak wygląda stopniowe obciążenia pręta siłą ściskającą

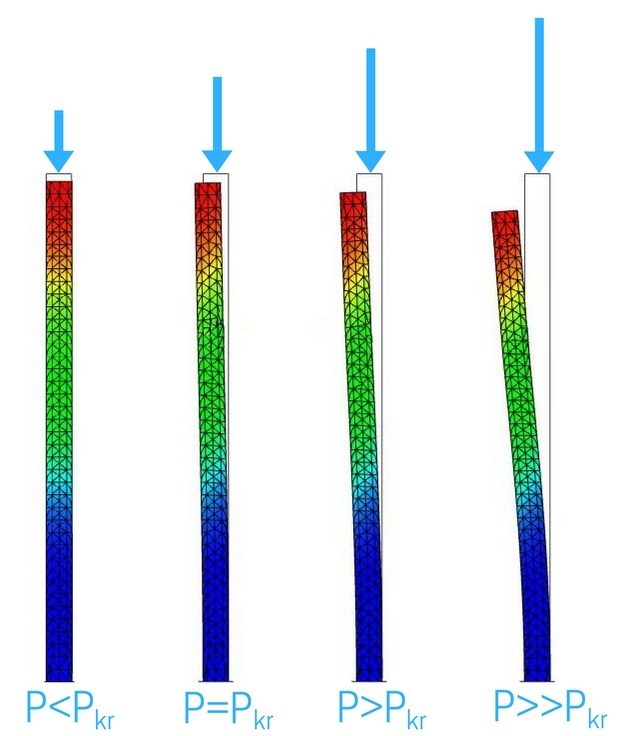
idąc od lewej:

Fig. 1 – siła mniejsza od siły krytycznej (pręt się tylko skraca)

Fig. 2 – siła ma wartość siły krytycznej zgodnie z obliczeniami powyżej (pręt zaczyna ulegać wyboczeniu)

Fig. 3 – siła większa od siły krytycznej (widoczne wyboczenie pręta)

Fig. 4 – siła większa od siły z Fig. 3 (bardzo widoczne wyboczenie pręta)

Zgodnie z naszymi przewidywaniami – analiza komputerowa MES wybaczania pręta pokazała, że pręt po przekroczeniu siły krytycznej zacznie się wybaczać 👍

Podsumowanie – stateczność prętów i wyboczenie prętów

Mam nadzieję, że jeśli nie rozumiałeś wcześniej stateczności prętów i wyboczenia prętów to ten artykuł pomógł Ci załapać o co w tym biega 😀. Dowiedziałeś się czym jest utrata stateczności prętów oraz jak obliczyć w różnych przypadkach siłę krytyczną i naprężenia krytyczne dla wyboczenia prętów. Poznałeś też parametr smukłości prętów i wiesz już, jak liczyć wyboczenia w zależności od stanu w którym znajduje się pręt (tj. czy stosować wzór Eulera, czy wzory aproksymujące).

Pamiętaj, że będąc konstruktorem, czy 💡wynalazcą 💡 wyboczenie jest bardzo istotnym aspektem, który należy uwzględnić podczas projektowania wszelkiego rodzaju konstrukcji mechanicznych i budowlanych. Złe dobranie grubości i przekroje profilów podczas projektowania, może przynieść opłakane skutki. Przy budowie wysokich budynków, rakiet czy mostów, należy zwrócić szczególną uwagę możliwość ich wyboczenia i przedsięwziąć odpowiednie środki by mu zapobiec.

Jeśli potrzebujesz POMOCY w konstruowaniu swoich wynalazków, czy prostszych mechanizmów odezwij się do nas, a na pewno razem jakoś podziałamy! >SZYBKI KONTAKT<